Heads up No Limit by Will Tipton
- By Will Tipton
- May 18, 2014
- Comments Off on Heads up No Limit by Will Tipton
Excerpt Expert Heads up No Limit Hold’em, Volume 1
Now, let us review a few more specifics. We can organize all of the possible decisions in a HUNL hand into a decision tree made up of decision points linked together by player actions. Each point in the tree, except for the leaves, which represent the end of a hand, represents a particular state of the game and is a spot where a player (or Nature) has to make a decision. The game will move into one of several new states depending on the choice. We saw that the full decision tree representing HUNL at any appreciable stack size is too large to handle. However, there is a lot to learn from approximate games. For example, a tree representing a river situation where there is just one bet left in the remaining stacks is shown in the figure.
A player’s strategy specifies how he will make any decision he can face in a game. In practice, a strategy must specify the range of hands with which the player takes each action at each of his decision points. We can visualize this as follows. Both players start the hand with a range consisting of 100% of each of the 1,326 distinct hold ’em hands. At each of his decision points, a player partitions or splits his range into several portions, one for each of his strategic options. In this way, a player’s range tends to get smaller and more clearly defined as the players get deeper and deeper into a hand. This splitting of ranges is illustrated in the “sun-burst” tree on the cover of this book.
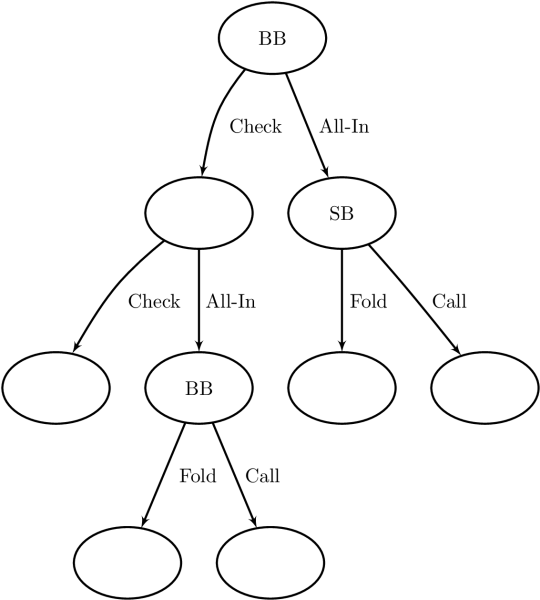
Figure: Decision tree representing river play with one bet left behind.
The expected value or EV of a holding for a player at a particular decision point is his total stack size at the end of the hand, averaged over all the ways the hand can play out from that point onward. Remember that our convention for EV is different than that of some other authors. We work in terms of total stack sizes, as opposed to changes in stack sizes. The basic approach to decision-making at any point is to consider the EV of each of our available options and then go with the largest. A best response or maximally exploitative strategy is one that maximizes a player’s EV in this way with every hand in every spot. Given a game described by a decision tree and Villain’s strategy for playing that game, we saw how to compute Hero’s best response in Chapter 2.
When both players are employing maximally exploitative strategies simultaneously, we have a Nash equilibrium. When two players adopt their equilibrium strategies in HUNL, neither has any incentive to deviate. They cannot improve their expectations by doing so, since they are already playing maximally exploitatively. An equilibrium strategy is also known as unexploitable, since it is the best a player can do against an opponent who is aware of his strategy and capable of quickly adjusting to it. When two sufficiently smart players face each other, they can do no better than to play their equilibrium strategies. Thus, when we find a game’s equilibrium, we say we have solved it. In this book, we use the terms GTO, unexploitable, and equilibrium as synonyms to refer to such strategies.
A solution for the full game of HUNL is not known, but the result of an attempt to get close is called pseudo-optimal or near-optimal play. We have seen that pseudo-optimal play is appropriate not only against mind-reading super-geniuses, but also against more run-of-the-mill opponents whose strategies are simply unknown to us. When facing a new opponent, many different exploitative strategies could be best depending on his tendencies. When these tendencies are unknown, however, any deviation from GTO play on our part is just about as likely to hurt as to help us. Without knowledge of a player’s weaknesses, we cannot expect any particular deviation from equilibrium to increase our EV. Although it is not entirely rigorous, we can think of unexploitable play as our best response given complete uncertainty about our opponent.
Furthermore, understanding unexploitable play can help us recognize exploitable tendencies in our opponents and understand how to adjust our own ranges to take advantage. For example, recall one of the simplest river situations we looked at in Volume 1: the PvBC game. One player’s range is made up of the nuts and air, and his opponent holds only hands that beat the air but lose to the nuts. We saw that under many conditions, the equilibrium strategies here are for the first player to bet all-in with all of his nut hands and enough bluffs so that his opponent’s EV if he calls is the same as if he folds. Similarly, the second player’s GTO play is to call enough to keep the first indifferent to bluffing.
What about exploitative play? If the polar player bluffs a bit too much, his opponent should always call, but if he bluffs even slightly too little, the bluff-catcher should always fold. On the other hand, if the bluff-catcher calls too much, his opponent should never bluff, and vice versa. Of course, “too much” and “too little” are defined in terms of the unexploitable strategies. So, our understanding of GTO play makes it very easy to understand and describe all of the opportunities for exploitative play in this situation. Despite the fact that HUNL’s true equilibrium is likely too large to memorize and too complicated to fully understand (and not even the best approach versus most opponents), the players with the best knowledge of game-theoretic play are also some of the best exploitative players because of their understanding of the game. With this in mind, we have focused on learning about equilibrium strategies to develop intuition and understanding of the structure of HUNL play. In this volume, we will continue our careful consideration of a variety of spots and how we might want to split our ranges when we encounter them.
Although we will describe refinements later, our general approach to match play begins by playing pseudo-optimally. From this defensive posture, Hero can observe his opponent’s tendencies and determine appropriate adjustments. Of course, it is rare that a new opponent is a complete unknown. In practice, we may do well to make some pre-game adjustments based on our knowledge of population tendencies – the tendencies of an average individual in our player pool. However, this caveat does not give us a free pass to just make “standard” plays without good reason. Any deviation from equilibrium play should be justified by reference to a particular exploitable tendency, whether of the population on average or of a particular opponent.
Although this is a book on heads up play, it’s worth noting that many of the properties that make Nash equilibria so useful do not hold in games with three or more players. In particular, if we play an equilibrium strategy in HUNL, we are guaranteed to at least break even (neglecting rake) on average over both positions. That is not the case in 3-or-more player games, where playing an equilibrium strategy provides no lower bound on our expected winnings. Thus, the Nash equilibrium is much less useful outside of heads up play, and anyone selling the idea of “GTO” strategies for 3-or-more player games should be viewed with suspicion.



